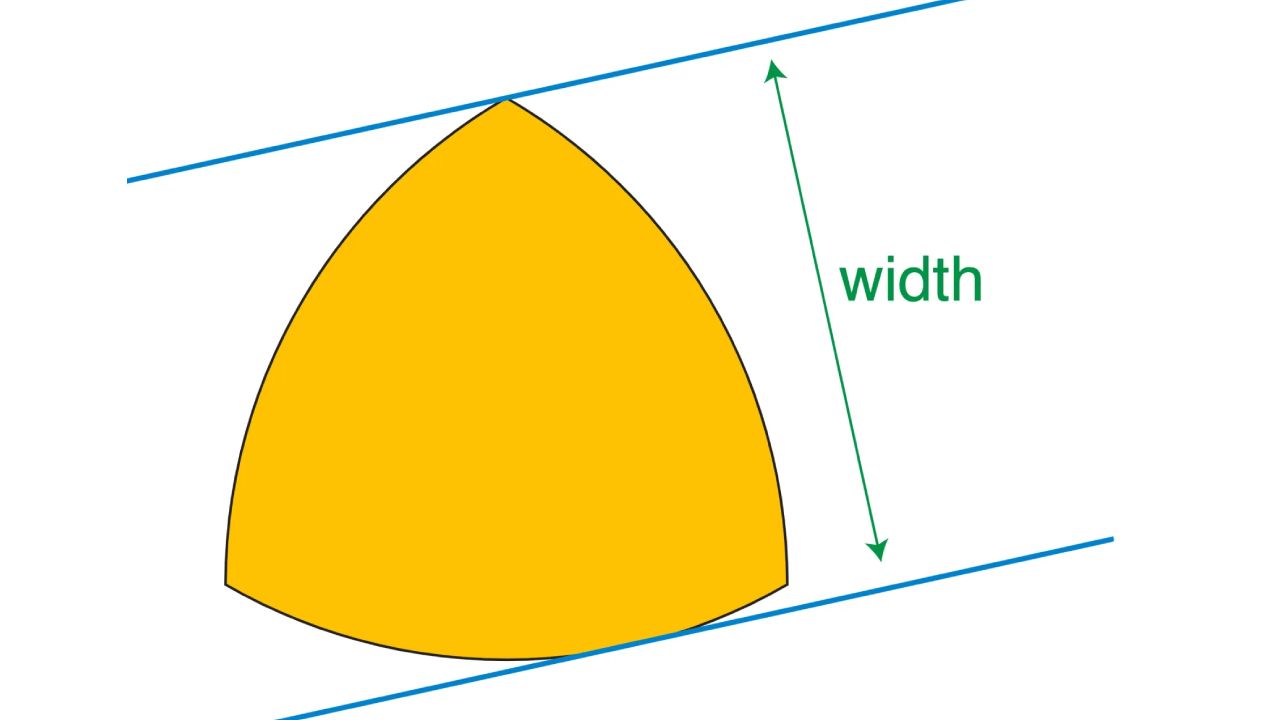
Bu şeklin iki boyutlu versiyonu Reuleaux üçgeni olarak adlandırılıyor. Üçgen, her köşesini birbirine bağlayan eğimli yaylara sahip, aynı genişliğe sahip bir daireden daha küçük bir alana ve sabit genişliğe sahip bir şekil oluşturan eşkenar üçgen olarak tanımlanabilir. Matematikçilerden oluşan bir ekip, artık bu şekli üçüncü boyuta ve ötesine ölçeklendirdiklerini ve bunun 1988’den bu yana varlığını sürdüren bir matematik problemini çözdüğünü söylüyor. Orijinal problem, daha yüksek boyutlu bir küreden daha küçük, sabit genişliğe sahip nesnelerin var olup olamayacağını sorgulayan matematikçi Oded Schramm tarafından sunulmuştu. Ekibin araştırması şu anda ön baskı sunucusu arXiv’de yer alıyor.
REULEAUX ÜÇGENİ
Adını bir 19. yüzyıl mühendisinden alan ancak çok daha öncesinde Euler ve Leonardo da Vinci gibi bilim insanları tarafından kullanılan Reuleaux üçgeni, birbiriyle kesişen üç dairenin yerleştirilmesiyle oluşturulabilir ve bu dairelerin ortasında kalan boşluk Reuleaux üçgenini oluşturur. 1914 ve 1915’te ilgili matematikçiler tarafından bağımsız olarak yayınlanan Blaschke-Lebesgue teoremi, üçgenin belirli bir sabit genişlikteki tüm eğriler arasında en az alana sahip olduğunu belirtiyordu. Başka bir deyişle, şeklin kenarları boyunca çizeceğiniz herhangi iki paralel arasındaki mesafe, yani genişliği her zaman sabit olacaktır. Bu şekil, iki boyutta bir Reuleaux üçgeni oluşturuyor. Üç boyutta ise dikdörtgenimsi ve hala beynimizin görselleştirebileceği bir şekil oluşturuyor. Ekip, üçüncü boyutun ötesinde, artan boyutlarda bile şeklin sabit genişliğini matematiksel olarak yansıtabildiğini belirtiyor.
Manitoba Üniversitesi matematikçisi ve araştırmanın ortak yazarı Andriy Prymark, “bu oluşumda başarılı olmamızın nedenlerinden biri belki de vücutlarımızın bir bakıma ‘dengesiz’ olması ve büyük miktarda hacmin belirli yerlerde dışa itilmesidir” diyor ve ekliyor: “Bu şekilde vücut daha az küreye benziyor ve aynı genişlikte daha küçük hacim elde edilmesine imkan tanıyor.”
New Scientist’in de bildirdiği üzere, daha yüksek boyutlarda şekil, eşdeğer boyuttaki üst boyutlu kürelerden orantılı olarak daha küçük oluyor. Ayrıca, tam bir yuvarlak olmasa da bir tekerlek gibi rahatça dönebiliyor.